AI Math
1강. 벡터가 뭐에요
벡터는 숫자를 원소로 가지는 리스트 또는 배열이다.
벡터를 수식과 코드로 표현하면 아래와 같다. 왼쪽은 열 벡터, 오른쪽은 행 벡터라고 부른다.

numpy.array를 가지고 벡터를 표현한다. 코드로 표현할 때에는 보통 행 벡터로 표현한다. (행 벡터를 기준으로 함)
벡터 안의 원소의 갯수를 벡터의 차원이라고 한다.
벡터는 공간에서의 한 점을 나타내며(어떤 차원에서든), 원점으로부터 상대적인 위치를 표현한다. 이러한 벡터에 숫자 또는 스칼라를 곱해주면 벡터의 길이를 변형시키는 것이 가능하다.
벡터끼리는 여러 가지 연산을 할 수 있다.
벡터끼리 같은 모양을 가진다면, 덧셈 / 뺄셈 / 성분곱을 계산할 수 있다. 다른 모양이라면 불가능하다.
이러한 연산들은 위 코드를 사용하여 + / - / * 으로 간단하게 구현할 수 있다.
두 벡터의 덧셈과 뺄셈은 다른 벡터로부터 상대적인 위치이동을 표현한다.
벡터의 노름(norm)은 원점에서부터의 거리를 말한다. 노름은 L1, L2노름이 있다. 이러한 노름은 임의의 차원인 d에 대해 성립한다. (벡터의 차원과 상관없이 계산 가능하다.)
L1노름은 각 성분의 변화량의 절대값을 모두 더하는 것이다. x, y좌표축을 따라서 이동하는 것과 같다.

L2노름은 피타고라스 정리를 이용해 유클리드 거리를 계산한다. 원점으로부터 좌표까지 바로 이동하는 것과 같다.

노름은 종류에 따라서 기하학적 성질이 달라진다. 그 이유는 거리의 정의를 다르게 했기 때문이다.

머신러닝에서 사용되는 목적에 따라 두 가지 방법을 모두 사용한다.
L1, L2 노름을 이용해서 두 벡터 사이의 거리를 계산할 수 있다. 이는 두 점 사이의 거리를 구하는 것과 같다.
두 벡터 사이의 거리를 계산할 때는 벡터의 뺄셈을 이용한다.
이렇게 계산된 거리를 이용하여 두 벡터 사이의 각도도 계산할 수 있다. 제 2 코사인 법칙을 사용하면 가능하다.

제 2 코사인 법칙에서의 분자는 두 벡터의 내적으로 표현할 수 있다.
np.inner(x, y)를 사용한다면, 코드 상에서 내적을 표현가능하다. 이런식으로 구한 값은 코드 상의 np.arccos(v)를 통해 각도를 구할 수 있게 된다.
단, 각도를 구하는 것은 L2노름에서만 가능하다.
내적은 정사영(orthogonal projection)된 벡터의 길이와 관련이 있다. 정사영된 벡터의 길이는 코사인 법칙에 의해서 한 벡터의 길이 * cos값이 된다. 이러한 정사영된 길이를 다른 벡터 y의 길이만큼 조정한 값이 된다.
2강. 행렬이 뭐에요
행렬(matrix)은 벡터를 원소로 가지는 2차원 배열이다. 수식과 코드로 나타내면 아래와 같다.

소문자 볼드체로 표기할 경우, 벡터를 표시하는 것이지만, 대문자 볼드체로 표현할 경우, 행렬을 표시하는 것이다.
행렬은 행(row)과 열(column)이라는 인덱스(idnex)를 가진다.
전치행렬(transpose matrix)은 행과 열의 인덱스가 바뀐 행렬이다. 전치행렬을 표현하는 방법은 오른쪽과 같다.

행렬은 공간에서의 여러 점들을 나타낸다. 행렬의 행벡터는 i 번째 데이터를 의미하는 것과 같다.
행렬끼리 같은 모양을 가지면 덧셈 / 뺄셈 / 성분곱 을 계산할 수 있다. 또한, 스칼라곱도 벡터와 동일하게 가능하다.
행렬의 곱셈은 i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다. 계산은 다음과 같이 한다.

행렬의 곱셈은 X행렬의 열의 개수와 Y행렬의 행의 개수가 같아야 한다. 행렬의 곱셈은 순서가 매우 중요하다. 이 순서가 바뀌면 값이 달라지거나 연산이 불가능할 수도 있다.
행렬의 내적은 np.inner를 사용하여 계산가능하다. 이는 i 번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다. 수학에서 말하는 내적과는 다르다.

행렬의 내적은 두 행렬의 행벡터들의 크기가 같아야만 계산이 가능하다. 다른경우는 불가능하다.
행렬은 벡터공간에서 사용되는 연산자로 이해할 수 있다. 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있으며, 패턴을 추출하고 데이터를 압축할 수도 있다.
모든 선형변환은 행렬곱으로 계산할 수 있다.
역행렬(inverse matrix)은 어떤 행렬 A의 연산을 거꾸로 되돌리는 행렬이다. 이는 행과 열 숫자가 같고, 행렬식(determinant)이 0이 아닌 경우에만 계산 가능하다.
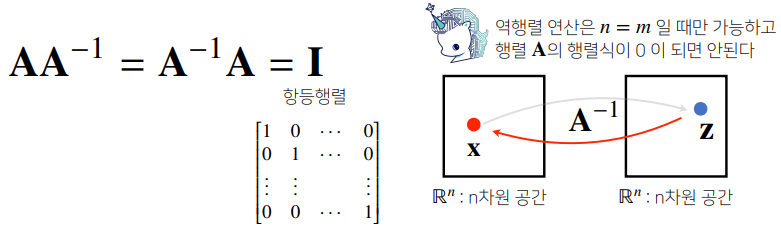
행렬에 역행렬을 곱하면 항등행렬(identity matrix)이 결과로 나오게 된다.
numpy로 역행렬과 항등행렬을 구하는 방법은 다음과 같다. llinalg 라이브러리를 사용한다.
X = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
# 역행렬 구하기
np.linalg.inv(X)
# 항등행렬 구하기
X @ np.linalg.inv(X)
만약, 행과 열이 같지 않은 경우에는 역행렬 대신 어떤 것을 사용할까?
이 때에는 역행렬 대신 유사역행렬(pseudo-inverse)를 사용한다. 이는 다른 이름으로 무어-펜로즈 역행렬(Moore-Penrose) 이라고 한다. 이는 행과 열의 숫자가 달라도 계산할 수 있다. 이 때에는 역행렬을 나타내는 -1 기호가 아닌, + 기호를 사용해서 표현한다.
이와 같이 표현한다면, 행과 열의 숫자가 달라도, 역행렬과 완전히 똑같지는 않지만, 역행렬과 유사한 기능을 하는 행렬을 나타낼 수 있다.
이 때, 조심할 점이 있다. 주어진 행렬에서 행의 갯수가 더 많은 경우와, 열의 갯수가 더 많은 경우에 따라 유사 역행렬을 구하는 방식이 달라진다.

numpy에서 유사역행렬을 구하는 코드는 linalg.pinv 라이브러리를 사용해서 구한다.
Y = np.array([[0, 1],
[1, -1],
[-2, 1]])
# 유사 역행렬 구하기
np.linalg.pinv(Y)
# 항등행렬 구하기
np.linalg.pinv(Y) @ Y
조심할 점은,
회고
AI Math 부분에서는 통계학이 조금 어렵게 느껴졌다. 강의를 들으며 몰랐던 부분과 잘 아는 부분과의 차이를 확실하게 알 수 있었고, 내가 무엇을 더 공부해야하는지에 대한 답이 명확하게 느껴졌다.
위 내용은 부스트캠프 AI Tech 에서 제공한 내용을 바탕으로 작성하였습니다.
'부스트캠프 AI Tech' 카테고리의 다른 글
| 3주차 - 최적화 (0) | 2022.10.05 |
|---|---|
| 3주차 - 딥러닝 기본 (0) | 2022.10.04 |
| 2주차 - PyTorch 구조 학습하기 (0) | 2022.09.30 |
| 2주차 - Pytorch 기본 (0) | 2022.09.29 |
| 1주차 - Python (9/19 ~ 9/23) (1) | 2022.09.23 |