본 내용은 도서 '딥러닝 텐서플로 교과서'의 내용을 참고했습니다.
출처 : http://www.yes24.com/Product/Goods/100295267?OzSrank=1
github : https://github.com/gilbutITbook/080263
1. 지도학습
지도학습 : 정답을 컴퓨터에 미리 알려 주고 데이터를 학습시키는 방법
- 분류(classification) : 주어진 데이터를 정해진 범주에 따라 분류
- 회귀(regression) : 데이터들의 특성을 기준으로 연속된 값을 그래프로 표현
K-최근접 이웃(K-Nearest Neighbor)
주어진 데이터에 대한 분류를 수행하기 위해 사용한다. 직관적이며 사용하기 쉽고, 훈련 데이터셋을 충분히 확보할 수 있는 환경에서 사용하면 좋다.

K-최근접 이웃 : 새로운 입력(분류되지 않은 검증 데이터)을 받았을 때, 기존 클러스터에서 모든 데이터와 인스턴스 기반 거리를 측정한 후 가장 많은 속성을 가진 클러스터에 할당하는 분류 알고리즘
K 값의 선택에 따라 새로운 데이터에 대한 분류 결과가 달라질 수 있음
[예제 : 붓꽃에 대한 분류]
데이터셋 : https://archive.ics.uci.edu/ml/machine-learning-databases/iris/
라이브러리 호출 및 데이터 준비
# 벡터 및 행렬의 연산 처리를 위한 라이브러리
import numpy as np
# 데이터를 차트나 플롯으로 그려 주는 라이브러리
import matplotlib.pyplot as plt
# 데이터 분석 및 조작을 위한 라이브러리
import pandas as pd
# 모델 성능 평가
from sklearn import metrics
# 데이터 셋에 열(column) 이름 할당
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
# 데이터를 판다스 프레임워크에 저장, 경로는 수정
dataset = pd.read_csv('./chap3/data/iris.data', names = names)
훈련과 검증 데이터셋 분리
# 모든 행을 사용하지만, 열(컬럼)은 뒤에서 하나를 뺀 값을 가져와서 X에 저장
X = dataset.iloc[:, :-1].values
# 모든 행을 사용하지만 열은 앞에서 다섯 번째 값만 가져와서 y에 저장
y = dataset.iloc[:, 4].values
from sklearn.model_selection import train_test_split
# X, y를 사용하여 훈련과 검증 데이터셋으롭 분리하며, 검증 세트의 비율은 20%만 사용
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
from sklearn.preprocessing import StandardScaler
# 특성 스케일링(scaling), 평균이 0, 표준편차가 1이 되도록 변환
s = StandardScaler()
# 훈련 데이터와 검증 데이터를 스케일링 처리
X_train = s.transform(X_train)
X_Test = s.transform(X_test)
모델 생성 및 훈련
from sklearn.neighbors import KNeighborsClassifier
# K = 50인 K-최근접 이웃 모델 생성
knn = KNeighborsClassifier(n_neighbors = 50)
# 모델 훈련
knn.fit(X_train, y_train)
모델 정확도 측정
from sklearn.metrics import accuracy_score
y_pred = knn.predict(X_test)
prnit("정확도 : {}".format(accuracy_score(y_test, y_pred)))정확도: 0.9333333333333333
위와 같은 결과가 출력된다.
최적의 K 찾기
k = 10
acc_array = np.zeros(k)
# K는 1에서 10까지 값을 취함
for k in np.arange(1, k+1, 1):
# for문을 반복하면서 K값 변경
classifier = KNeighborsClassifier(n_neighbors = k).fit(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = metrics.accuracy_score(y_test, y_pred)
acc_array[k-1] = acc
max_acc = np.array(acc_array)
acc_list = list(acc_array)
k = acc_list_index(max_acc)
print("정확도", max_acc, "으로 최적의 k는", k+1, "입니다.")정확도 1.0 으로 최적의 k는 1 입니다.위와 같은 결과가 나온다.
K가 50일 때는 정확도가 93%였지만, K가 1일 때는 정확도가 100%로 높아졌다. K값에 따라 성능이 달라지므로 초기 설정이 매우 중요하다.
서포트 벡터 머신(SVM)
주어진 데이터에 대한 분류를 할 때 사용한다. SVM은 분류를 위한 기준선을 정의하는 모델로, 커널만 적절히 선택한다면 정확도가 꽤 좋기 때문에, 정확도를 요구하는 분류 문제에 적합하다. 또한, 텍스트를 분류할 때에도 사용한다.
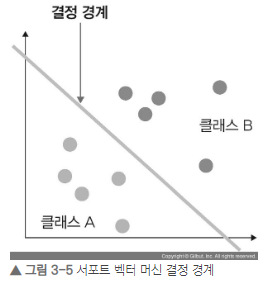
결정 경계 : 데이터를 분류하기 위한 기준선
결정 경계는 데이터가 분류된 클래스에서 최대한 멀리 떨어져 있을 때 성능이 가장 좋다.
마진(margin) : 결정 경계와 서포트 벡터 사이의 거리
서포트 벡터(support vector) : 결정 경계와 가까이 있는 데이터
최적의 결정 경계는 마진을 최대로 해야한다.

마진을 최대화 할 때, 이상치를 잘 다루어야 한다.
하드 마진(hard margin) : 이상치를 허용하지 않는 것
소프트 마진(soft margin) : 어느 정도의 이상치들이 마진 안에 포함되는 것을 허용하는 것
위 그림은 하드 마진의 예이다.
[예제 : 붓꽃에 대한 분류]
라이브러리 호출
from sklearn import svm
from sklearn import metrics
from sklearn import datasets
from sklearn import model_selection
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3' -TF_CPP_MIN_LOG_LEVEL이라는 환경 변수를 사용해서 로깅을 제어한다.
- 0 : 기본값으로, 모든 로그가 표시됨
- 1 : INFO 로그를 필터링
- 2 : WARNING 로그를 필터링
- 3 : ERROR 로그를 추가로 필터링
iris 데이터를 준비하고 훈련과 검증 데이터셋으로 분리
# 사이킷런에서 제공하는 iris 데이터 호출
iris = datasets.load_iris()
# 데이터셋 분리
X_train, X_test, y_train, y_test =
model_selection.train_test_split(iris.data, iris.target, test_siez = 0.6, random_state = 42)
SVM 모델에 대한 정확도
# SVM 분류기 제작
svm = svm.SVC(kernel = 'linear', C = 1.0, gamma = 0.5)
# 훈련 데이터를 사용하여 SVM 분류기를 훈련시킴
svm.fit(X_train, y_train)
# 훈련된 모델을 사용하여 검증 데이터에서 예측
predictions = svm.predict(x_test)
score = metrics.accuracy_score(y_test, predictions)
print('정확도 : {0.f}'.format(score))정확도: 0.988889
SVM은 선형 분류와 비선형 분류를 지원한다.
- 선형 커널(linear kernel) : 선형으로 분류 가능한 데이터에 적용. 선형 커널은 기본 커널 트릭으로 커널 트릭을 사용하지 않음
- 다항식 커널(polynomial kernel) : 실제로는 특성을 추가하지 않지만, 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있는 방법. 이를 통해 고차원으로 데이터 매핑이 가능함
- 가우시안 RBF 커널(Gaussian RBF kernel) : 다항식 커널의 확장이다. 다항식 커널과는 달리, 차수에 제한 없이 무한한 확장이 가능하다.
위의 SVM 분류기 제작 부분에서 C 값은 오류를 어느 정도 허용할 지 지정하는 파라미터이다. C값이 클 수록 하드 마진이고, 작을수록 소프트 마진이다.
gamma는 결정 경계를 얼마나 유연하게 가져갈지 결정한다. 이 값이 높으면 훈련 데이터에 많이 의존하여 엄청나게 복잡한 곡선 형태를 띠어 과적합이 발생할 수 있으니 조심하도록 하자.
결정 트리(decision tree)
주어진 데이터에 대한 분류를 할 때 사용한다. 결정 트리는 데이터를 분류하거나 결과 값을 예측하는 분석 방법으로서, 이상치가 많은 값으로 구성된 데이터셋을 다룰 때 사용하기 좋다. 또한, 그 과정이 시각화로 잘 되어있어 유용하다.

결정 트리는 데이터를 분류한 후, 각 영역의 순도는 증가, 불순도와 불확실성은 감소하는 방향으로 학습 진행한다.
순도 증가, 불확실성 감소 ☞ 정보획득
결정 트리에서 불확실성을 계산하는 방법
- 엔트로피(entropy) : 확률 변수의 불확실성을 수치로 나타낸 것이다. 높을수록 불확실성이 높다.
- 지니계수(Gini index) : 불순도를 측정하는 지표로서, 데이터의 통계적 분산 정도를 정량화해서 표현한 값이다.(원소 n개 중에서 임의로 두 개를 추출하였을 경우, 추출된 두 개가 서로 다른 그룹에 속해 있을 확률) 지니계수가 높을수록, 데이터가 분산되어 있다.
[예제 : 타이타닉 승객의 생존 여부 예측하기]
라이브러리 호출 및 데이터 준비
데이터 : https://github.com/gilbutITbook/080263/tree/master/chap3/data/titanic
import pandas as pd
# 판다스를 이용하여 train.csv 파일 로드 후, df에 저장
df = pd.read_csv("./chap3/data/titanic/train.csv", index_col = 'PassengerId')
# 상위 5개 행 출력
print(df.head())
데이터 전처리
데이터 분석에 필요한 컬럼만 추출하자
# 승객의 생존 여부를 예측하기 위해 아래와 같은 column 사용
df = df[['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Survived']]
# 성별을 나타내는 'sex'를 0, 1로 변환
df['Sex'] = df['Sex'].map({'male' : 0, 'female' : 1})
# 값이 없는 데이터 전부 삭제
df = df.dropna()
X = df.drop('Survived', axis = 1)
# y값은 예측 label
y = df['Survived']
훈련과 검증 데이터 셋으로 분리
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 1)
결정 트리 모델 생성
from sklearn import tree
model = tree.DecisionTreeClassifier()
모델 훈련
model.fit(X_train, y_train)
모델 예측
y_predict = model.predict(X_test)
from sklearn.metrics import accuracy_score
# 검증 데이터에 대한 예측 결과
accuracy_score(y_test, y_predict)0.8379888268156425출력 결과가 83%로 좋은 학습결과를 보여주고 있다.
혼동 행렬을 이용한 성능 측정
from sklearn.metrics import confusion_matrix
pd.DataFrame(
confusion_matrix(y_test, y_predict),
columns = ['Predicted Not Survival', 'Predicted Survival'],
index = ['True Not Survival', 'True Survival']
)| Predicted Not Survival | Predicted Survival | |
| True Not Survival | 99 | 13 |
| True Survival | 16 | 51 |
위는 혼동 행렬에 대한 출력결과이다.
혼동 행렬은 알고리즘 성능 평가에 사용된다. 의미는 아래와 같다.
| 예측 값 | |||
| Positive | Negative | ||
| 실제 값 | Positive | TP | FN |
| Negative | FP | TN | |
- TP (True Positive) : 모델이 1이라고 예측했고, 실제 값도 1인 경우
- TN (True Negative) : 모델이 0이라고 예측했고, 실제 값도 0인 경우
- FP (False Positive) : 모델이 1이라고 예측했고, 실제 값이 0인 경우
- FN (False Negative) : 모델이 0이라고 예측했고, 실제 값은 1인 경우
이들을 가지고 여러 가지 성능 지표로 활용할 수 있다.
결정 트리를 확대한 것은 랜덤 포레스트이다.
로지스틱 회귀와 선형 회귀
회귀란, 변수가 두 개 주어졌을 때, 한 변수에서 다른 변수를 예측하거나, 두 변수의 관계를 규명하는데 사용하는 방법이다.
- 독립 변수(예측 변수) : 영향을 미칠 것으로 예상되는 변수
- 종속 변수(기준 변수) : 영향을 받을 것으로 예상되는 변수
로지스틱 회귀
분석하고자 하는 대상들이 두 집단, 혹은 그 이상으로 나누어질 때, 개별 관측치들이 어느 집단에 분류될 수 있는지 분석하고, 이를 예측하는 모형을 개발하는데 사용되는 통계기법이다. 주어진 데이터에 대한 확신이 없거나, 추가적으로 train dataset을 수집할 수 있는 환경에서 사용하면 좋다.
종속 변수 : 이산형 변수, 모형 탐색 방법 : 최대 우도법, 모형 검정 : X^2 테스트
분석 절차는 다음과 같다.
- 각 집단에 속하는 확률의 추정치 예측
- 분류 기준 값을 설정한 후 특정 범주로 분류
[예제 : 신규 데이터(숫자) 예측]
라이브러리 호출 및 데이터 준비
데이터셋 : 사이킷런에서 제공
%matplotlib inline
from sklearn.datasets import load_digits
digita = load_digits()
# digits 데이터셋의 형태이다. 이미지 = 179개, 8 x 8 이미지의 64차원
print("Image Data Shape", digits.data.shape)
# 레이블 이미지 1797개
print("Label Data Shape", digits.target_shape)Image Data Shape (1797, 64)
Label Data Shape (1797,)
digits 데이터셋의 시각화
import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize = (20, 4))
# 이미지 5개만 확인
for index, (image, label) in enumerate(zip(digits.data[0:5], digits.target[0:5])):
plt.subplot(1, 5, index + 1)
plt.imshow(np.reshape(image, (8, 8)), cmap = plt.cm.gray)
plt.title("Training : %i \n" % label, fontsize = 20)
훈련과 검증 데이터셋 분리 및 로지스틱 회귀 모델 생성
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(digits.data, digits.target,
test_size = 0.5, random_state = 0)
from sklearn.linear_model import LogisticRegression
# 로지스틱 회귀 모델의 인스턴스 생성
logisticRegr = LogisticRegression()
# 모델 훈련
logisticRegr.fit(x_train, y_train)
일부 데이터를 사용한 모델 예측
# 새로운 이미지에 대한 예측 결과 출력(넘파이 형태)
logisticRegr.predict(x_test[0].reshape(1, -1))
# 이미지 10개에 대한 예측 출력(배열)
logisticRegr.predict(x_test[0:10])
전체 데이터를 사용한 모델 예측
# 전체 데이터셋에 대한 예측
predictions = logisticRegr.predict(x_test)
# 스코어 메서드를 사용한 성능 측정
score = logisticRegr.score(x_test, y_test)
print(score)0.9511111111111111
혼동 행렬 시각화
import numpy as np
import seaborn as sns
from sklearn import metrics
# 혼동 행렬
cm metrics.confusion_matrix(y_test, predictions)
plt.figure(figsize = (9, 9))
# heatmap으로 표현
sns.heatmap(cm, annot = True, fmt = ".3f", linewidths = .5, square = True, cmap = 'Blues_r')
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
all_sample_title = 'Accuracy Score : {0}'.format(score)
plt.title(all_sample_title, size = 15)
plt.show()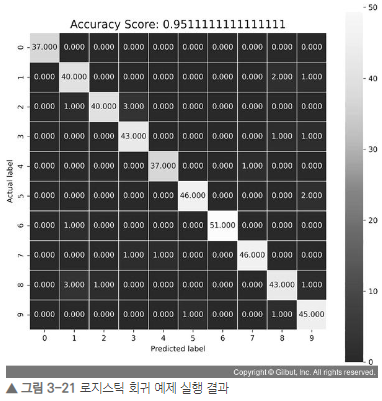
선형 회귀
독립 변수 x를 사용하여, 종속 변수 y의 움직임을 예측하고 설명하는데 사용한다. 이 두 변수가 선형 관계를 가질 때 사용하면 유용하다. 또한, 독립 변수가 변경되었을 때, 종속 변수를 추정하는데 유용하다. 독립 변수는 여러개 일 수 있다.
로지스틱 회귀와 선형 회귀의 차이점은 아래와 같다.
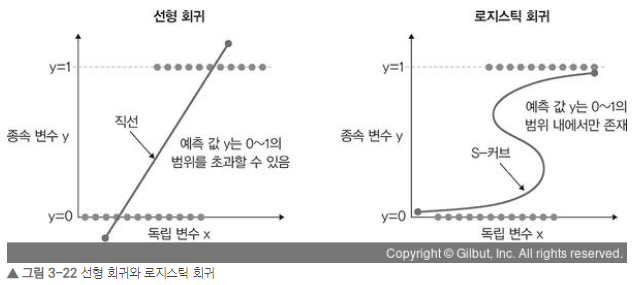
[예제 : 날씨 예측]
데이터셋 : 캐글에서 제공하는 날씨 데이터셋 이용(https://www.kaggle.com/akdagmelih/rain-prediction-logistic-regression-example/data?select=weatherAUS.csv)
라이브러리 호출
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as seaborninstance
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics
%matplotlib inline
데이터셋 불러오기
dataset = pd.read_csv('./chap3/data/weather.csv')
데이터 간 관계를 시각화로 표현
datasets.plot(x='MinTemp', y='MaxTemp', style = 'o')
plt.title('MinTemp vs MaxTemp')
plt.xlabel('MinTemp')
plt.ylable('MaxTemp')
plt.show()
데이터를 독립 변수와 종속 변수로 분리하고 선형 회귀 모델 생성
X = dataset['MinTemp'].values.reshape(-1, 1)
y = dataset['MaxTemp'].values.reshape(-1, 1)
# 데이터셋 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
# 선형 회귀 클래스 가져오기
regressor = LinearRegression()
# 모델 훈련
regressor.fit(X_train, y_train)
회귀 모델에 대한 예측
y_pred = regressor.predict(X_test)
df = pd.DataFrame({'Actual' : y_test.flatten(), 'Predicted' : y_pred.flatten()})
df
검증 데이터셋을 사용한 회귀선 표현
plt.scatter(X_test, y_test, color = 'gray')
plt.plot(X_test, y_pred, color = 'red', linewidth = 2)
plt.show()
선형 회귀 모델 평가
print('평균제곱법:', metrics.mean_squared_error(y_test, y_pred))
print('루트 평균제곱법:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))평균제곱법: 17.011877668640622
루트 평균제곱법: 4.124545753006096'Deep Learning > 딥러닝 텐서플로 교과서' 카테고리의 다른 글
| 3-2. 머신 러닝 핵심 알고리즘 - 비지도학습 (0) | 2022.08.02 |
|---|---|
| 2. 텐서플로 기초 (0) | 2022.08.01 |
| 1. 머신러닝과 딥러닝 (0) | 2022.08.01 |