본 내용은 도서 '딥러닝 텐서플로 교과서'의 내용을 참고했습니다.
http://www.yes24.com/Product/Goods/100295267?OzSrank=1
github : https://github.com/gilbutITbook/080263
2. 비지도학습
비지도 학습은, 지도 학습처럼 정답 값이 필요하지 않으며, 정답이 없는 상태에서 훈련시키는 방식이다. 비지도 학습에는 다음과 같은 방법이 있다.
- 군집(clustering) : 각 데이터의 유사성(거리)을 측정한 후, 유사성이 높은(거리가 짧은) 데이터끼리 집단으로 분류. 주요 알고리즘으로는 K-평균 군집화(K-Means)가 있다.
- 차원 축소(dimensionality reduction) : 차원을 나타내는 특성을 줄여 데이터를 줄이는 방식. 주요 알고리즘으로는 주성분 분석(PCA)가 있다.
주성분 분석(PCA)
고차원 데이터를 저차원(차원 축소) 데이터로 축소시키는 알고리즘이다. 데이터의 특성이 너무 많을 때, 특성 두세개로 압축해서 데이터를 시각화할 때 사용한다.
차원 축소 방법
- 데이터들의 분포 특성을 잘 설명하는 벡터를 두 개 선택
- 벡터 두 개를 위한 적정한 가중치를 찾을 때까지 학습을 진행
PCA는 데이터 하나하나에 대한 성분을 분석하는 것이 아닌, 여러 데이터가 모여 하나의 분포를 이룰 때, 분포의 주성분을 분석하는 방법이다.
[예제 : 훈련 데이터를 정확하게 클러스터링 하기]
데이터 : https://github.com/gilbutITbook/080263
라이브러리 호출
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 밀도 기반 군집 분석
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import normalize
from sklearn.decomposition import PCA
데이터 불러오기
X = pd.read_csv('./chap3/data/credit card.csv')
# 해당 컬럼 삭제
X = X.drop('CUST_ID', axis = 1)
# 결측치를 다음 값으로 채우기
X.fillna(method = 'fill', inplace = True)
print(X.head())
데이터 전처리 및 데이터를 2차원으로 차원 축소
scaler = StandScaler()
# 평균 0, 표준편차 1되도록 데이터 크기 조정
X_scaled = scaler.fit_transform(X)
# 데이터가 가우스 분포를 따르도록 정규화
X_normalized = normalize(X_scaled)
# 넘파이 배열을 DF로 변환
X_normalized = pd.DataFrame(X_normalized)
# 2차원으로 차원 축소 선언
pca = PCA(n_components = 2)
# 차원 축소 적용
X_principal = pca.fit_transform(X_normalized)
X_principal = pd.DataFrame(X_principal)
X_principal.columns = ['P1', 'P2']
print(X_principal.head()) P1 P2
0 -0.489949 -0.679976
1 -0.519099 0.544827
2 0.330633 0.268880
3 -0.481656 -0.097611
4 -0.563512 -0.482506
DBSCAN 모델 생성 및 결과의 시각화
# 모델 생성 및 훈련
db_default = DBSCAN(eps=0.0375, min_samples=3).fit(X_principal)
# 각 데이터 포인트에 할당된 모든 클러스터 레이블의 넘파일 배열을 labels에 저장
labels = db_default.labels_
# 출력 그래프의 색상을 위한 레이블 생성
colours = {}
colours[0] = 'y'
colours[1] = 'g'
colours[2] = 'b'
colours[-1] = 'k'
# 각 데이터 포인트에 대한 색상 벡터 생성
cvec = [colours[label] for label in labels]
r = plt.scatter(X_principal['P1'], X_principal['P2'], color='y');
g = plt.scatter(X_principal['P1'], X_principal['P2'], color='g');
b = plt.scatter(X_principal['P1'], X_principal['P2'], color='b');
# 플롯(plot)의 범례(legend) 구성
k = plt.scatter(X_principal['P1'], X_principal['P2'], color='k');
plt.figure(figsize=(9,9))
# 정의된 색상 벡터에 따라 X축에 P1, Y축에 P2 플로팅(plotting)
plt.scatter(X_principal['P1'], X_principal['P2'], c=cvec)
# 범례 구축
plt.legend((r, g, b, k), ('Label 0', 'Label 1', 'Label 2', 'Label -1'))
plt.show()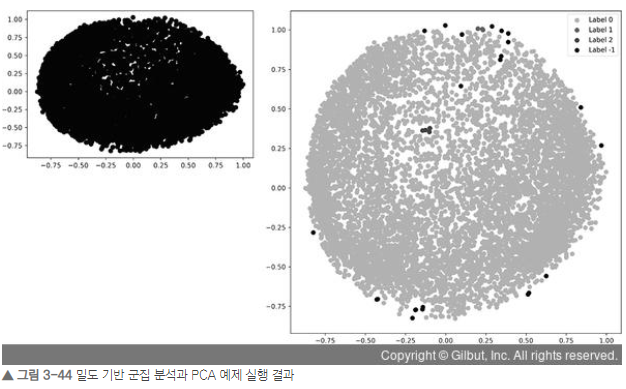
클러스터링에 대한 튜닝이 필요해보인다.
모델 튜닝
db = DBSCAN(eps=0.0375, min_samples=50).fit(X_principal)
labels1 = db.labels_
colours1 = {}
colours1[0] = 'r'
colours1[1] = 'g'
colours1[2] = 'b'
colours1[3] = 'c'
colours1[4] = 'y'
colours1[5] = 'm'
colours1[-1] = 'k'
cvec = [colours1[label] for label in labels1]
colors1 = ['r', 'g', 'b', 'c', 'y', 'm', 'k']
r = plt.scatter(
X_principal['P1'], X_principal['P2'], marker='o', color=colors1[0])
g = plt.scatter(
X_principal['P1'], X_principal['P2'], marker='o', color=colors1[1])
b = plt.scatter(
X_principal['P1'], X_principal['P2'], marker='o', color=colors1[2])
c = plt.scatter(
X_principal['P1'], X_principal['P2'], marker='o', color=colors1[3])
y = plt.scatter(
X_principal['P1'], X_principal['P2'], marker='o', color=colors1[4])
m = plt.scatter(
X_principal['P1'], X_principal['P2'], marker='o', color=colors1[5])
k = plt.scatter(
X_principal['P1'], X_principal['P2'], marker='o', color=colors1[6])
plt.figure(figsize=(9,9))
plt.scatter(X_principal['P1'], X_principal['P2'], c=cvec)
plt.legend((r, g, b, c, y, m, k),
('Label 0', 'Label 1', 'Label 2', 'Label 3', 'Label 4', 'Label 5', 'Label -1'),
scatterpoints=1,
loc='upper left',
ncol=3,
fontsize=8)
plt.show()
모델 튜닝 결과이다. 군집이 잘 보인다.
밀도 기반 군집 분석 모델의 하이퍼파라미터인자를 변경하여 그래프 출력
db = DBSCAN(eps=0.0375, min_samples=100).fit(X_principal)
이처럼 최적의 성능을 내기 위해서는 하이퍼파라미터를 이용한 튜닝이 중요하다.
K-평균 군집화
데이터를 입력받아 소수의 그룹으로 묶는 알고리즘이다. 레이블이 없는 데이터를 입력받아 각 데이터에 레이블을 할당해서 군집화를 수행한다.
학습과정은 다음과 같다.
- 중심점 선택 : 랜덤하게 초기 중심점을 선택한다.
- 클러스터 할당 : K개의 중심점과 각각의 개별 데이터 간의 거리를 측정한 후, 가장 가까운 중심점을 기준으로 데이터를 할당한다.
- 새로운 중심점 선택 : 클러스터마다 새로운 중심점을 계산한다.
- 범위 확인 : 선택된 중심점에 더 이상의 변화가 없다면, 진행을 멈춘다. 변화가 있다면, 맨 처음으로 돌아가 과정을 반복한다.
데이터가 비선형일 경우와 군집 크기가 다를 경우, 군집마다 밀집도와 거리가 다를 경우에는 원하는 결과와 다르게 발생할 수 있기때문에 사용하지 않는 것이 좋다.
[예제 : 적절한 K 값 찾기]
데이터 : https://github.com/gilbutITbook/080263
라이브러리 호출
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
상품에 대한 연 지출 데이터 호출
data = pd.read_csv('../chap3/data/sales data.csv')
data.head()
데이터셋
- Channel: 고객 채널(호텔/레스토랑/카페) 또는 소매 채널(명목형 데이터)
- Region: 고객 지역(명목형 데이터)
- Fresh: 신선한 제품에 대한 연간 지출(연속형 데이터)
- Milk: 유제품에 대한 연간 지출(연속형 데이터)
- Grocery: 식료품에 대한 연간 지출(연속형 데이터)
- Frozen: 냉동 제품에 대한 연간 지출(연속형 데이터)
- Detergents_Paper: 세제 및 종이 제품에 대한 연간 지출(연속형 데이터)
- Delicassen: 조제 식품에 대한 연간 지출(연속형 데이터)
연속형 데이터와 명목형 데이터(범주형 데이터)로 분류
# 명목형 데이터
categorical_features = ['Channel', 'Region']
# 연속형 데이터
continuous_features = ['Fresh', 'Milk', 'Grocery', 'Frozen', 'Detergents_Paper', 'Delicassen']
for col in categorical_features:
# 명목형 데이터는 판다스의 get_ dummies() 메서드를 사용하여 바이너리로 변환
dummies = pd.get_dummies(data[col], prefix=col)
data = pd.concat([data, dummies], axis=1)
data.drop(col, axis=1, inplace=True)
data.head()
연속형 데이터를 스케일링하기위해서는 MinMaxScaler()를 사용한다.
mms = MinMaxScaler()
mms.fit(data)
data_transformed = mms.transform(data)
적당한 K값 추출
Sum_of_squared_distances = []
K = range(1, 15)
for k in K:
km = KMeans(n_clusters=k)
km = km.fit(data_transformed)
Sum_of_squared_distances.append(km.inertia_)
plt.plot(K, Sum_of_squared_distances, 'bx-')
plt.xlabel('k')
plt.ylabel('Sum_of_squared_distances')
plt.title('Optimal k')
plt.show()
밀도 기반 군집 분석(DBSCAN)
일정 밀도 이상을 가진 데이터를 기준으로 군집을 형성하는 방법이다. 노이즈에 영향을 받지 않으며, K-평균 군집화에 비해 연산량이 많긴하지만, 잘 처리하지 못하는 오목하거나 볼록한 부분을 처리하는데 유용하다.


노이즈 : 주어진 데이터셋과 무관하거나 무작위성 데이터로, 전처리 과정에서 제거해주어야함
이상치 : 관측된 데이터 범위에서 많이 벗어난 아주 작은 값이나 아주 큰 값을 의미함
밀도 기반 군집 분석 방법은 다음과 같다.
- 앱실론 내 점 개수 확인 및 중심점 결정
- 군집 확장
- 앞의 두 개의 단계 반복. 더이상 중심점을 정의할 수 없을 때까지 반복함
- 어떤 군집에도 포함되지 않은 데이터를 노이즈로 정의한다.
'Deep Learning > 딥러닝 텐서플로 교과서' 카테고리의 다른 글
| 3-1. 머신 러닝 핵심 알고리즘 - 지도학습 (0) | 2022.08.02 |
|---|---|
| 2. 텐서플로 기초 (0) | 2022.08.01 |
| 1. 머신러닝과 딥러닝 (0) | 2022.08.01 |